哈特利振荡器是经典的LC反馈电路之一,用于产生高频波形或信号。正如我们在LC振荡器一文中讨论的那样,如果反馈网络中的电抗元件 X1 和 X2 选择为电感,而 X3 为电容,则该振荡器被称为哈特利振荡器。
这些振荡器可以通过不同的电路配置来实现。�哈特利振荡器的主要部分是放大器部分和谐振部分。谐振部分由两个电感和一个电容组成。每个部分对交流信号电压产生180度的相移,因此它产生正弦波电压。
哈特利振荡器电路
哈特利振荡器的电路图如下图所示。一个以共发射极配置连接的NPN晶体管作为放大器阶段的有源器件。R1 和 R2 是偏置电阻,RFC是射频扼流圈,它提供了交流和直流运行之间的隔离。
在高频下,该扼流圈的电抗值非常高;因此,它可以被视为开路。对于直流条件,电抗为零,因此不会对直流电容造成问题。CE 是发射极旁路电容,RE 也是一个偏置电阻。电容 CC1 和 CC2 是耦合电容。
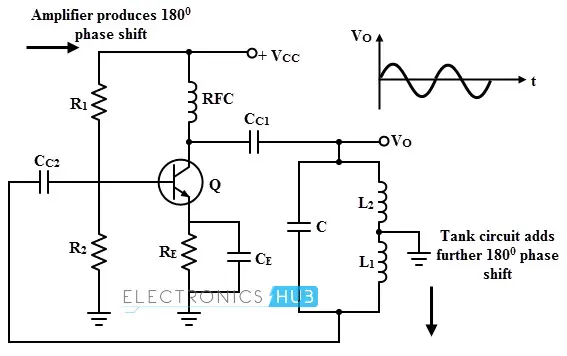
当给电路施加直流电源(Vcc)时,集电极电流开始上升并开始对电容 C 充电。一旦 C 完全充电,它开始通过 L1 和 L2 放电,然后再次开始充电。
这种来回的电压波形是正弦波,它很小,并且以负半波领先。除非它被放大,否则它最终会消失。
现在晶体管开始发挥作用。由谐振电路产生的正弦波通过电容 CC1 耦合到晶体管的基极。
由于晶体管被配置为共发射极,它从谐振电路中获取输入,并将其反转为具有正半波领先的标凈正弦波。
因此,晶体管提供了放大和反转,以放大并修正由谐振电路产生的信号。L1 和 L2 之间的互感提供了从集电极 - 发射极电路到基极 - 发射极电路的能量反馈。
该电路的振荡频率为
f0=2πLeqC1
其中 Leq 是谐振电路中线圈的总电感,由下式给出
Leq=L1+L2+2M
对于实际电路,如果 L1=L2=L 并且忽略互感,则振荡频率可以简化为
f0=2π2LC1
在某些电路中,存在一个晶体管化的哈特利振荡器的 L1 和 L2 之间的互感,如下图所示。

哈特利振荡器中的互感
一个线圈中的电流变化通过磁场在附近另一个线圈中感应出电流,这种现象称为互感。这是由于一个电感的磁通量在另一个电感中引起的额外电感量。
考虑到互感的影响,线圈的总电感可以通过以下公式计算:
Leq=L1+L2+2M
其中 M 是互感,其值取决于电感之间的有效耦合、它们之间的间距、每个线圈的尺寸、每个线圈的匝数以及用于共同磁芯的材料类型。
在射频振荡器中,根据紧密耦合电感产生的磁场的南北极性,确定电路的总电感。
如果各个线圈产生的磁场方向相同,则互感将增加总电感,从而使总电感增加。
如果磁场方向相反,则互感将减少总电感。因此,振荡器的工作频率将增加。
哈特利振荡器的设计考虑了这两个电感的相互影响。在实际应用中,两个电感通常使用一个共同的磁芯,然而,根据耦合系数,互感的影响可能会更大。
当电感之间存在100%的磁耦合时,这个系数值为1,如果电感之间没有磁耦合,则其值为0。
使用运算放大器的哈特利振荡器电路
可以使用运算放大器实现哈特利振荡器,其典型配置如下图所示。这种类型的电路便于通过反馈电阻和输入电阻调整增益。
在晶体管化的哈特利振荡器中,增益取决于谐振电路元件 L1 和 L2,而在运算放大器振荡器中,增益较少依赖于谐振电路元件,因此提供了更好的频率稳定性。
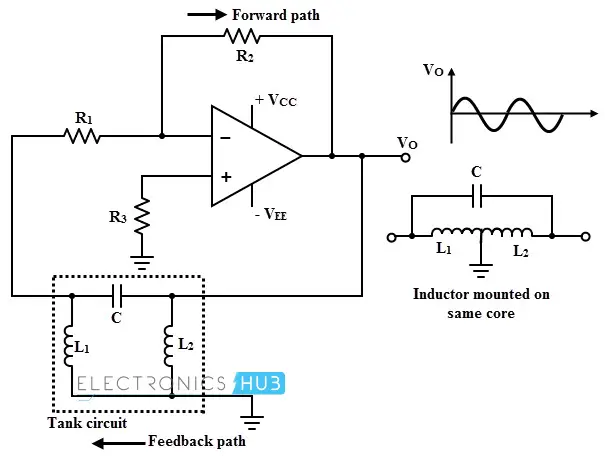
该电路的工作原理与晶体管版本的哈特利振荡器类似。由反馈电路产生的正弦波与运算放大器部分耦合。然后,该波形由放大器稳定并反转。
通过在谐振电路中使用可变电容来改变振荡器的频率,同时保持反馈比和输出幅度在频率范围内恒定。这种振荡器的振荡频率与上述讨论的振荡器相同,由下式给出:
f0=2πLeqC1
其中 Leq=L1+L2+2M 或 L1+L2
为了从该电路产生振荡,放大器增益必须大于或至少等于两个电感的比值。
Av=L2L1
如果由于这两个线圈的共同磁芯存在 L1 和 L2 之间的互感,则增益变为
Av=L2+ML1+M
示例1
假设一个晶体管化的哈特利振荡器的谐振电路具有100 pF的电容。集电极和抽头点之间的电感为30 µH,抽头点和晶体管基极之间的电感为1×10⁻⁸ H。求振荡频率。忽略互感。
已知:
C=100 pF=100×10−12 F
L1=30 μH=30×10−6 H
L2=1×10−8 H
晶体管化哈特利振荡器的振荡频率由下式给出:
f0=2π(L1+L2)C1
=2π((30×10−6)+(1×10−8))×100×10−121
=2.9×106 Hz
=2.9 MHz
示例2
考虑下图,其中使用运算放大器和反馈LC网络构建了哈特利振荡器。根据给定的值,确定工作频率和电阻 R 的最大可接受值,以便开始振荡。

对于哈特利振荡器,振荡频率由下式给出:
f0=2πLeqC1
其中 Leq=L1+L2
Leq=1.0×10−6+0.1×10−6=1.1×10−6
给定的电容值为 C=1×10−9 F
因此,
f0=2π1.1×10−6×1×10−91=4.799 MHz
反馈因子为:
L1L2=1.0×10−60.1×10−6=0.1
因此,所需的最小增益为10。
然而,增益为
增益=RR2=R100×103
因此,R 的最大值为
R=10100×103=10 kΩ
- 可以使用一根单根的裸线圈代替两个独立的线圈 L1 和 L2,并将线圈在任意期望的点接地。
- 通过使用可变电容或使磁芯可移动(改变电感),可以调节振荡频率。
- 在工作频率范围内,输出幅度保持恒定。
- 所需的元件非常少,包括两个固定的电感或一个抽头线圈。
- 由于电感值较大且电感体积庞大,它不能用作低频振荡器。
- 该振荡器的输出中谐波含量非常高,因此它不适用于需要纯净正弦波的应用。

